En física, el condensado de Bose-Einstein es el estado de agregación de la materia que se da en ciertos materiales a temperaturas cercanas al cero absoluto.1 La propiedad que lo caracteriza es que una cantidad macroscópica de las partículas del material pasan al nivel de mínima energía, denominado estado fundamental. El condensado es una propiedad cuántica que no tiene análogo clásico. Debido al principio de exclusión de Pauli, sólo las partículas bosónicas pueden tener este estado de agregación: si las partículas que se han enfriado son fermiones, lo que se encuentra es un líquido de Fermi.
En la década de 1920, Satyendra Nath Bose y Albert Einstein publican conjuntamente un artículo científico acerca de los fotones de luz y sus propiedades. Bose describe ciertas reglas para determinar si dos fotones deberían considerarse idénticos o diferentes. Esta se llama la estadística de Bose (o a veces la estadística de Bose-Einstein). Einstein aplica estas reglas a los átomos preguntándose cómo se comportarían los átomos de un gas si se les aplicasen estas reglas. Así descubre los efectos que vienen del hecho de que a muy bajas temperaturas la mayoría de los átomos están al mismo estado cuántico, que sería el menos energético posible.
Imagínese una taza de té caliente, las partículas que contiene circulan por toda la taza. Sin embargo cuando se enfría y queda en reposo, las partículas tienden a ir en reposo hacia el fondo. Análogamente, las partículas a temperatura ambiente se encuentran a muchos niveles diferentes de energía. Sin embargo, a muy bajas temperaturas, una gran proporción de éstas alcanza a la vez el nivel más bajo de energía, el
estado fundamental.
La agrupación de partículas en ese nivel inferior se le llama Condensado de Bose-Einstein (BEC), porque la demostración está hecha de acuerdo con las ecuaciones de Einstein. Lo que seguramente no pudo imaginar es lo extraño que se vería una masa de materia con todos sus átomos en un solo nivel. Esto significa que todos los átomos son absolutamente iguales. No hay medida que pueda diferenciar uno de otro. Se trata de un estado de coherencia cuántica microscópico.
Desarrollo teórico de la condensación de Bose-Einstein. Sea un gas de metano degenerado (esto es, alejado de la aproximación clásica de la estadística de Maxwell-Boltzmann y, por tanto, donde tiene relevancia la distinción entrefermiones y bosones). Considérese que los únicos grados de libertad son traslacionales.
El número medio de partículas en un estado cuántico

(o número de ocupación) viene dado por:
Esta función vale infinito cuando el argumento de la exponencial vale cero y cae rápidamente. Esto es debido a que los bosones no cumplen el
principio de exclusión de Pauli y por tanto puede haber infinidad de ellos en el mismo estado cuántico individual.
Si el sistema tiene

partículas, entonces debe cumplirse que la suma de todas las partículas que se encuentren en cada estado cuántico

debe dar el total.
Si el sistema es cerrado, la relación
[2] nos sirve para definir el
potencial químico 
.
Supóngase además que el mínimo nivel de energía accesible a una partícula es

. Esto es admisible ya que coincide con el menor valor de la energía que puede tener un gas de partículas con grados traslacionales de libertad.
Esta imposición obliga a que

. De no ser así, entonces habría estados cuya energía sería menor que el potencial químico y resultaría que los números medios de ocupación serían una cantidad negativa lo cual no es posible.
Supóngase que la diferencia entre dos niveles consecutivos de energía es tan pequeña que se puede cambiar el
sumatorio por una
integral.
Conviene separar el cálculo del número total de partículas en dos partes, una que de cuenta de aquellas cuyo valor de la energía es el propio del estado fundamental, y otro distinta de cero, estados excitados. De no hacerlo se llegaría a una contradicción, como se vera.
El número de partículas cuya energía es distinta de cero viene dada por la siguiente expresión, donde

es la
distribución de probabilidad que nos dice cuantas partículas tienen su energía comprendida entre

y

.
Se puede demostrar que la distribución de probabilidades viene dada por:
siendo

el grado de degeneración,

el volumen del sistema,

la
constante de Planck,

la masa de los bosones y

la energía.
De tal manera que,

Utilizando que:

para x > 1.
donde:
Se llega a que:
De modo que:
Es el número máximo de partículas que el sistema puede tener a una temperatura dada en los estados excitados, llamado

.
Esto permite definir la llamada temperatura de Bose, o temperatura crítica, en la cual:

. La función de Riemman está acotada:

, así:
siendo una relación de igualdad el caso límite o crítico. Ese caso límite se da a la temperatura crítica

:

Si se hubiera tomado únicamente la expresión [3], se tendría que:
Lo cual haría que en

no pudiera existir un gas de bosones, lo cual contradice la experiencia. Por eso se ha dividido el cálculo en dos partes.
Si se divide la ecuación [3] por la densidad total del sistema se obtiene que:
A temperaturas mucho mayores que

, este cociente es mayor que la unidad. Eso significa que nuestro sistema admite más bosones en los estados excitados de los que se tienen actualmente.
A temperaturas menores que

el cociente es menor que la unidad. Eso significa que muchas de las partículas constituyentes de nuestro sistema se han ido al estado fundamental al no poder haber tantas en los estados excitados.
Es el otro sumando, el número de partículas en el estado fundamental. En

se verifica que

de modo que:
Este fenómeno se conoce como condensación de Bose-Einstein. La denominación puede inducir a error pues no se trata de una
condensación como un gas normal. Cuando un gas ideal clásico cambia de estado gaseoso a líquido se dice que se condensa, en ese caso disminuye su volumen (o aumenta su densidad). En el condensado de Bose no hay disminución de volumen, las partículas se quedan quietas.
Si se dibujase en el
espacio fásico 
de posiciones y
momentos conjugados, el condensado de un gas corriente estaría agrupado cerca de
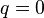
(eje horizontal) mientras que en el condensado de Bose esta agrupación se produce en torno a
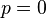
(eje vertical).
Obtención en laboratorio. Eric Cornell y Carl Wieman lograron en 1995 por primera vez, enfriar átomos al más bajo nivel de energía, menos de una millonésima de Kelvin por encima del cero absoluto, una temperatura muy inferior a la mínima temperatura encontrada en el espacio exterior. Utilizaron el método de enfriamiento por láser, haciendo que la luz rebote en los átomos con más energía que su impacto sobre los mismos. Cuando los fotones rebotan en el átomo, el electrón en el átomo que absorbe el fotón salta a un nivel superior de energía y rápidamente salta de regreso a su nivel original, expulsando el fotón de nuevo, logrando el descenso de su temperatura.
Para que ello suceda se necesita el color (o frecuencia) exacta de láser para la clase de átomo a enfriar. Finalmente, la sustancia se enfría aún más con la evaporación magnética de los átomos con más energía. Consiste en dejar escapar del confinamiento magnético a los átomos más energéticos, que al hacerlo se llevan consigo más energía de la que le corresponde, logrando así dejar dentro los de más baja temperatura.
Superfluidez y superconductividad. La superconductividad es un ejemplo de condensado. En ésta son los pares de Cooper (asociaciones de una pareja de electrones) los que se comportan como un bosón y decae al nivel fundamental. La superconductividad está caracterizada por la ausencia de resistencia eléctrica.
La
superfluidez es otro ejemplo de condensado. El helio cuando se enfría se licúa, si se sigue enfriando los átomos de helio (que son bosones) descienden al nivel de mínima energía, el 0 Kelvin. Esto hace que los átomos no adquieran energía por fricción, lo que hace que no se disipe energía por movimiento. El resultado es un plano horizontal infinitamente estrecho; como lo que pasa en el interior de las supernovas cuando su periodo vital se agota y se transforman en agujeros negros.
Se le atribuye un efecto cuántico macroscópico óptico al condensado Bose-Einstein de átomos de
sodio que, al inducirle electromagnéticamente el estado de translucidez, tiene la propiedad de reducir la velocidad de la luz en forma asombrosa. Hasta 20 millones de veces su velocidad en el vacío, equivalente a 17 metros por segundo (m/s).



















 (o número de ocupación) viene dado por:
(o número de ocupación) viene dado por:
 siendo
siendo  la
la  partículas, entonces debe cumplirse que la suma de todas las partículas que se encuentren en cada estado cuántico
partículas, entonces debe cumplirse que la suma de todas las partículas que se encuentren en cada estado cuántico 
 .
. . Esto es admisible ya que coincide con el menor valor de la energía que puede tener un gas de partículas con grados traslacionales de libertad.
. Esto es admisible ya que coincide con el menor valor de la energía que puede tener un gas de partículas con grados traslacionales de libertad. . De no ser así, entonces habría estados cuya energía sería menor que el potencial químico y resultaría que los números medios de ocupación serían una cantidad negativa lo cual no es posible.
. De no ser así, entonces habría estados cuya energía sería menor que el potencial químico y resultaría que los números medios de ocupación serían una cantidad negativa lo cual no es posible.
 es la
es la  y
y  .
.

 el grado de degeneración,
el grado de degeneración,  el volumen del sistema,
el volumen del sistema,  la
la  la masa de los bosones y
la masa de los bosones y 
 se tiene:
se tiene:
 para x > 1.
para x > 1. es la función
es la función  es la función
es la función  es la longitud de onda de De'Broglie:
es la longitud de onda de De'Broglie:

 .
. . La función de Riemman está acotada:
. La función de Riemman está acotada:  , así:
, así:
 :
: 

 no pudiera existir un gas de bosones, lo cual contradice la experiencia. Por eso se ha dividido el cálculo en dos partes.
no pudiera existir un gas de bosones, lo cual contradice la experiencia. Por eso se ha dividido el cálculo en dos partes.

 se verifica que
se verifica que  de modo que:
de modo que:![N_0 = N - N' \simeq N - N'_{max} = N \left( 1 - \frac{N'_{max}}{N} \right) = N \left[ 1 - \left(\frac{T}{T_0} \right)^{3/2} \right]](https://upload.wikimedia.org/math/b/7/a/b7aef188cbb89413b9e4510f0c4249b3.png)
 ,
,  . Es decir, los bosones se agrupan en el
. Es decir, los bosones se agrupan en el  de posiciones y
de posiciones y 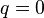 (eje horizontal) mientras que en el condensado de Bose esta agrupación se produce en torno a
(eje horizontal) mientras que en el condensado de Bose esta agrupación se produce en torno a 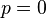 (eje vertical).
(eje vertical).